• Before demonstrating Ripley’s K function ($K(t)$), $L(t)$, and $H(t)$), I have to first simulate two types of point process: 1. Poisson point process and 2. Thomas point process.
  • The point process generator is adpated from Connor Johnson’s blog post.
  • The default size of point process generator is 20 x 20
  • Please visit the code on my GitHub
# denpendency 
import os, sys
import scipy.stats
import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.style
import matplotlib as mpl
import spatialstat.ppsim as ppsim
%load_ext autoreload
%autoreload 2

# define IO dir
path = '.'
opdir = os.path.join(path, 'output')
opdir_csv = os.path.join(opdir, 'csv')
opdir_fig = os.path.join(opdir, 'figure')

if not os.path.exists(opdir):
    os.makedirs(opdir)
if not os.path.exists(opdir_csv):
    os.makedirs(opdir_csv)
if not os.path.exists(opdir_fig):
    os.makedirs(opdir_fig)       
 
print(opdir)
print(opdir_csv)
print(opdir_fig)

./output
./output/csv
./output/figure

Poisson Point Process

  1. Create Poisson PP by ppsim.PoissonPP. Please visit the code on my GitHub
  2. export to *.csv
# Set seed
seed = 1219
rate = 1
Dx = 20

# set data range
xmin = 0 
xmax = Dx
ymin = 0
ymax = Dx

P_PoissonPP = ppsim.PoissonPP(rt = rate, seed = seed)
# calculate density
P_PoissonPP_density = ppsim.xydensity(P_PoissonPP)

# save to csv
filename = 'P_PoissonPP_' + str(Dx)
outputpath = os.path.join(opdir_csv, filename + '.csv')
df = pd.DataFrame(P_PoissonPP, columns = ['x', 'y']) 
df.to_csv(outputpath, index = False)

print("Size of the PoissonPP array: {}".format(P_PoissonPP.shape))
print("Density the PoissonPP array: {}".format(P_PoissonPP_density[0]))

Size of the PoissonPP array: (398, 2)
Density the PoissonPP array: 1.0070902229053578

Thomas Point Process

  1. Create Thomas PP from given parent points generated from Poison PP
  2. Create Thomas PP by ppsim.ThomasPP. Please visit the code on my GitHub
  3. export to *.csv
# Set seed
seed = 1219
rate = 0.1
Dx = 20

# create parent points
P_parent = ppsim.PoissonPP(rt = rate, seed = seed)
print("Size of the P_parent array: {}".format(P_parent.shape))

Size of the P_parent array: (39, 2)

# create children points
sigma = 0.3
mu = 50
P_children, P_parent = ppsim.ThomasPP(rt = rate,
                                sigma = sigma, mu = mu, seed = seed)
# reduce data to region of interest
xmin = 0 
xmax = Dx
ymin = 0
ymax = Dx

# crop data and calculate density
P_ThomasPP = ppsim.xyroi(P_children, xmin, xmax, ymin, ymax)
P_ThomasPP_density = ppsim.xydensity(P_ThomasPP) 

# save to csv
filename = 'P_ThomasPP_20'
outputpath = os.path.join(opdir_csv, filename + '.csv')
df = pd.DataFrame(P_ThomasPP, columns = ['x', 'y']) 
df.to_csv(outputpath, index = False)

print("Size of the ThomasPP array: {}".format(P_ThomasPP.shape))
print("Density the ThomasPP array: {}".format(P_ThomasPP_density[0]))

0 20 0 20
Size of the ThomasPP array: (1898, 2)
Density the ThomasPP array: 5.359077104022789

Plot Poisson and Thomas PP

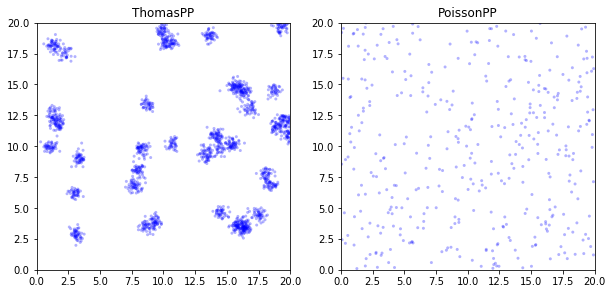
Now having point process we need, we can make plots and show them side-by-side.

# set figure size
plt.figure(figsize= (10, 10))
plotsize_x = 20.0
plotsize_y = 20.0

# subplot 1
plot_1 = plt.subplot(221)
plot_1.scatter(P_children[:, 0], P_children[:, 1], 
                color = 'b', edgecolors = 'none', marker = '.', alpha =0.3)
plot_1.set_title('ThomasPP')
plot_1.set_xlim([0,20])
plot_1.set_ylim([0,20])

# subplot 2
plot_2 = plt.subplot(222)
plot_2.scatter(P_PoissonPP[:, 0], P_PoissonPP[:, 1], 
                color = 'b', edgecolors = 'none', marker = '.', alpha =0.3)
plot_2.set_title('PoissonPP')
plot_2.set_xlim([0,20])
plot_2.set_ylim([0,20])

# save figure
filename = 'Point_Process_20'
outputpath = os.path.join(opdir_fig, filename + '.png')
plt.savefig(outputpath)

plt.show()

png

What Next…

In this simulation, it is easy to visually identify the clustering in Thomas Point Process. In the next post, I will demonstrate how to perfrom Ripley’s K test by using our customized code, so we measure the relationship of density and distance.